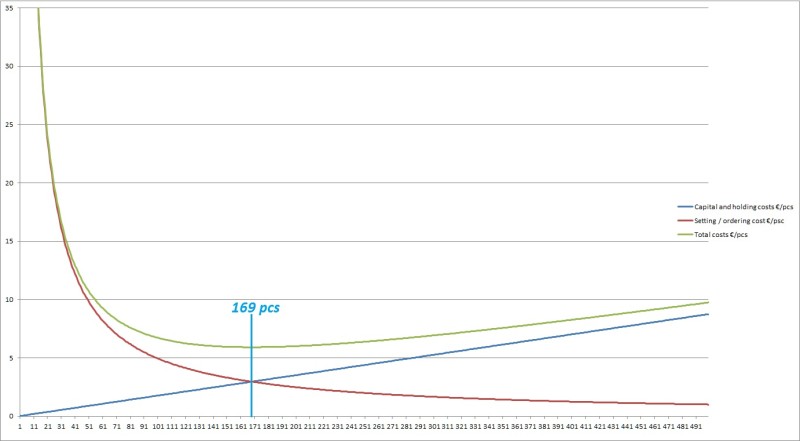
EOQ-kaavan alkuperä on teollisessa tuotannossa. Sen on alunperin kehittänyt Ford. W. Harris vuonna 1913. Hän huomasi, että vaihdettaessa valmistusta eri tuotteisiin syntyy hukkaa sekä kuluu aikaa asetusten tekemiseen. Suuremmat valmistusmäärät taasen sitovat pääomaa ja varastointitilaa. Alla on kuvio mitenkä pääomakulut ja asetuskulut jakautuvat erilaisille tuotantoerän määrille.
Kuvaajan oletuksena on, että tuotteen yksikkökustannus on 250 €, asetuskulu on 500 € ja varastointi- ja pääomakulu on 250 € * 10 % + 10 € = 35 €. Eli pääomakulun lisäksi lasketaan tuotteen vaatiman varastointitilan kustannuksen olevan 10 €/tuote. Oheisessa kuviossa yhteiskustannus sisältää vain nämä tilaus- ja varastointikustannukset, ei tuotteen varsinaista yksikkökustannusta, joka on vakio. Lähtölukujen muuttuessa taloudellinen tuotantoerä muuttuu, mutta kuvion ideana onkin selvittää millä tapaa nämä kustannukset vaikuttavat lopputulokseen. Kuvion muoto sinänsä ei muutu lähtöarvoja muutettaessa.
Vaihtoehto omalle tuotannolle on tuotteen ostaminen alihankkijalta, mutta alihankkija veloittaa tämän asetuskustannuksen ostajalta. Tämän takia sama kaava toimii myös taloudellisen/optimaalisen ostoerän hankkimiseen. Kaava ottaa huomioon tuotteen hinnan, kulutuksen, sisäisen korkokannan sekä tilauskustannuksen. Tuotteen hinta ja kulutus ovat helposti selvitettävissä ja sisäinen korkokanta on yrityksen johdon strateginen valinta. Isoin ongelma muodostuukin hankintakustannuksen määrittelemisestä.
Mitä kaikkia kustannuksia tuotteen hankinta- / tilauskustannus pitää sisällään? Lasketaanko siihen jonkun henkilön työtunnit? Jos henkilön toimenkuva on ostaja, jaetaanko hänen kuukausipalkkansa kuukaudessa tehtyjen ostotilausten määrällä? Pitäisikö tilaukselle laskea jonkinlainen keskimääräinen minuuttiaika, joka ostotilausten käsittelemiseen menee? Otetaanko kustannuksiin huomioon tilauksen vastaanotosta ja hyllyttämisestä syntyvät kustannukset?
Vaihtoehdot eivät varmastikaan olleet vielä tässä. Hankintakustannus näyttelee kuitenkin aika isoa osaa tässä kaavassa, joten sen määritteleminen on harkittava tarkoin ja mahdollisen myyjän tilauskustannuksen lisäksi on pohdittava tuleeko hankintakustannukseen sisällyttää myös joitakin tilauksesta aiheutuvia omia kuluja.
Kaavan oletukset
Kaavat sisältävät aina tiettyjä oletuksia. Tämän kaavan keskeisimmät oletukset ovat:
- Tuotanto tai osto tapahtuu heti, ei ole pullonkauloja saatavuuden tai kapasiteetin mukaan ja koko erän saa heti.
- Toimitus tapahtuu heti
- Kysyntä on varma ja vakaa
- Kysyntä noudattaa suoraa viivaa, vuosittainen kulutus voidaan jakaa 365 päivällä
- Asetus tai hankintakustannus on vakio riippumatta eräkoosta
Kaikki mallit noudattavat aina joitakin oletuksia. Reaalimaailma on paljon monimutkaisempi ja vaikeampi tulkita. Tämän vuoksi kaavan antamia lukuja ei tule tulkita pilkun tarkasti, vaan lopputulos tulee pyöristää esimerkiksi lähimpään pakkauskoon kerrannaiseen. Esimerkiksi joitakin pesuaineita myydään 6 kpl erissä, jotain tuotetta voidaan myydä 10 kpl erissä ja tölkkijuomia myydään yleisesti 24 kpl erissä. Olisi typerää tilata tölkkijuomia esimerkiksi 25 kpl, jolloin tukkuri joutuu purkamaan pakkauksen ja sen käsitteleminen on vaikeaa. Käsittelyvaurioiden ja muun yleisen helppouden vuoksi tulisi aina tilata täysiä pakkauksia.
EOQ-Kaava
Kaavassa:
- Q = Optimaalinen eräkoko
- P = Tilauskustannus (asetuskustannus)
- D = Vuosikulutus
- H = Varastointikustannus
- H voi olla jotain näistä:
- CV (C = korkokanta, V = tuotteen yksikkökustannus)
- CV + I (I = varastointikustannus)
Saamme eräkooksi 169 kpl, joka voidaan myös huomata ylläolevasta kuvaajasta. Siinä varastointikustannukset ja tilauskustannukset leikkaavat. Tässä kohdassa myös yhteiskustannus on pienimmillään. Voit laskea optimaalisen tilauserän myös täällä.
Kaavasta voidaan todeta, että optimaalinen tilauserä kasvaa tilauskustannuksen tai vuosikulutuksen neliöjuuressa. Vastaavasti se laskee varastointikustannusten neliöjuuressa. Tärkein huomio on kuitenkin Harris Fordin huomio, että varaston koon ja eräkoon väliltä löytyy kompromissi. Eräkoon kaasvattaminen kasvattaa varastoa, mutta toisaalta vähentää tilausmääriä.
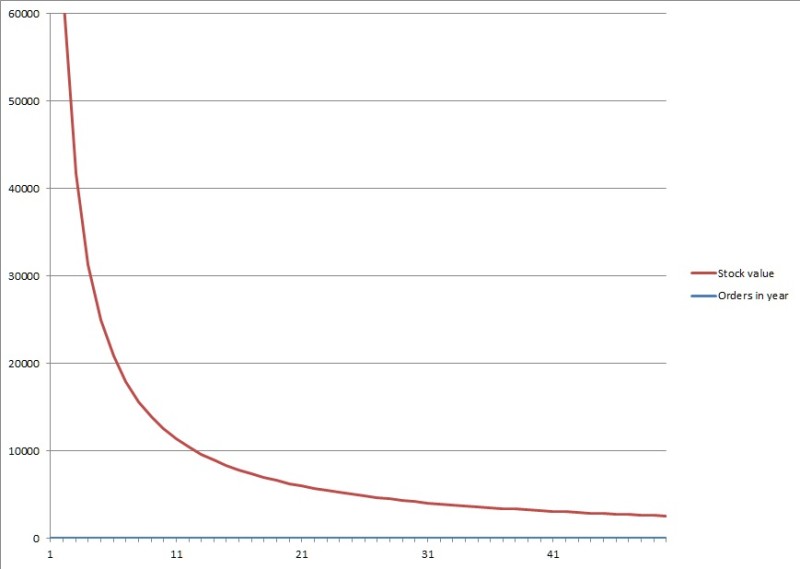
Alla olevassa kuviossa on tilaussyklin ja varaston arvon suhde. On huomattava, että vuositilausten muuttuessa 10 tilauksesta 20 tilaukseen varastoinvestoinnin arvo tippuu 12 500 eurosta puoleen, eli 6 250 euroon. Kuitenkin tilaussykliä tiuhentamalla 30 vuosittaiseen tilaukseen varaston arvo tippuu enää 33 % 4 167 euroon. Varaston arvo on kuitenkin laskeva eräkoon pienentyessä ja tilausmäärien kasvaessa.
Eräkoon muuttamisen vaikutus
Ylläolevassa esimerkissä eri eräkokojen kustannus pysyy 7 euron alapuolella eräkoon ollessa 94 – 306 kpl. Optimaalinen eräkoko kaavan mukaan olisi 169 kpl, jolloin yksikköhinnan päälle tuleva kustannus on 5,92 euroa. Eräkokoa voidaankin siis tässä esimerkissä muuttaa melko paljonkin kustannusten siitä paljoa muuttumatta.
Vuosittainen hankinta- ja pitokustannus erikokoisille erille saadaan näin:
- Y = Hankinta- ja pitokustannusten yhteenlaskettu vuosikustannus.
Josta voidaan johtaa EOQ-kaavaa hyväksikäyttäen kaava optimaaliselle vuosikustannukselle:
Meidän esimerkin mukainen optimaalinen eräkoko kustantaa meille 5916 € vuodessa.
Päätetyn eräkoon kustannuskerroin optimaaliseen eräkokoon verrattuna saadaan seuraavasta kaavasta:
- Qp = Tilattu eräkoko
- Qo = Optimaalinen eräkoko
Kaavasta saadaan selville, että tuplaamalla tai puolittamalla optimaalinen eräkoko, on oston kustannusvaikutus 25% optimaalisesta. Vastaavasti 20 % eräkoon muutoksella kustannusvaikutus on vain 1,7 %.
Optimaalinen tilaussykli on Q / D, eli tilauserä jaettuna vuosikulutuksella. Optimaalinen tilaussykli voidaan selvittää suoraan EOQ-kaavaa hyväksikäyttäen myös näin:

Ylläolevan esimerkin mukainen tilaussykli olisi 0,169 vuotta, eli 8,8 viikkoa tai 61,7 päivää. Tilaussyklin muutos optimaalisesta voidaan laskea samalla kaavalla kuin ylläolevassa esimerkissä eräkoon muutos optimaalisesta.
Mikäli yritys tilaa eri tuotteita samalta toimittajalta, kannattaa tilauksiin yhdistää tilausväli-mallia. Hopp suosittelee Factory Physics -kirjassa tilausväliksi kakkosen eksponentteja:
- 20 = 1 viikko
- 21 = 2 viikkoa
- 23 = 4 viikkoa
- 24 = 8 viikkoa
Vastaavasti nämä voivat olla myös päiviä, jos viikko on liian pitkä tilaussykli. Idena on se, että ostoerät keskitetään tälle tilausvälille, jolloin voidaan mahdollisesti yhdistää eri tuotteita samaan kuljetukseen ja säästetään kuljetuskustannuksissa.
Esimerkin optimaalinen tilaussykli olisi 8,8 viikkoa, mutta pyöristettäessä se lähimpään kakkosen potenssiin, saamme tilausväliksi 8 viikkoa eli 0,154 vuotta, jolloin tilauserä olisi 154 kpl.
154 kappaleen tilauserille meidän vuosikustannus olisi 5942 €, joka on alle prosentin päässä optimaalisesta 5916 eurosta. Mikäli tällä muutoksella pystytään yhdistelemään tuotteiden kuljetuksia, on muutos kannattava.
Tarkistuksena kustannuskerroin-kaavasta


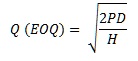




Optimaalinen tilaussykli on Q / D, eli tilauserä jaettuna vuosikulutuksella.
Eikö tämä mennyt väärinpäin?
Kyllä se on ihan oikein. Tarkistin sen tuossa vielä yksikkölaskennalla.
Jakamalla vuosikulutus (kpl/a) tilauserällä (kpl) saadaan montako kertaa vuodessa tavaraa tilataan. Eli yksiköt = (kpl/a) / kpl = 1/a = krt /vuosi. Tai kertomalla selkeämpi kpl/a * 1/kpl = 1/a.
Kun tilauserä (kpl) jaetaan vuosikulutuksella (kpl/a), saadaan tilaussykli. Tämän yksikkö on vuosia, jos laskussa käytetään vuosikulutusta.
kpl / (kpl/a) = a. Kertomalla kpl/1 * a/kpl = a.