
Yleisesti jonkin arvo n-vuoden päästä voidaan laskea allaolevalla kaavalla. Tämä pätee siis säästämiseen ja tällöin arvo kasvaa vuosien mittaan koron verran joka vuosi. Tätä sanotaan myös korkoa korolle -ilmiöksi, koska joka vuosi korolla kerrotaan pääoman ja edellisten korkojen yhteenlaskettu summa, ei ainoastaan alkuperäistä pääomaa.
- i = korko
- n = vuodet
Kun laskemme tulevien vuosien aikana saamamme rahan arvoa, meidän tulee diskontata se nykyarvoon. Koska ylläolevan kaavan mukaisesti rahan arvo kasvaa vuosittain koron verran, on tulevan rahan arvo nykypäivänä vähemmän kuin sen arvo tulevaisuudessa.
Investointilaskennassa lasketaankin monesti investoinnin tuottamien säästöjen nykyarvoa ja peilataan sitä investoinnin kustannukseen. Kaikki tulevat rahat muutetaan ensin nykyarvoon, jotta ne ovat vertailukelpoisia.
Jaksollinen maksu
Mikäli säästöt ovat joka vuosi samat, saamme kaikkien vuosien säästösumman nykyarvona seuraavasta jaksollisen maksun kertoimesta:
Esimerkiksi investointimme säästää meiltä 50 000 € vuosittain työ- ja materiaalikustannuksina. Investoinnin pitoaika on 10 vuotta ja yrityksen käyttämä laskentakorko on 12 %. Ylläolevasta kaavasta saamme selville, että jaksollisen maksun tekijä on 5,6502. Voimme siis laskea investoinnin tuottavan koko pitoaikanaan:
50 000 € * 5,6502 = 282 510 €.
Mikäli investoinnin hankinta-arvo on enemmän kuin 282 510 euroa, ei hankinta ole kannattava.
Yksittäinen maksu
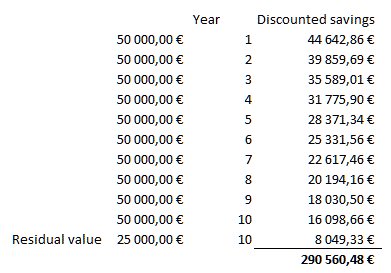
Mikäli vuosittaiset säästömme eivät ole tasaisia joka vuosi, joudumme laskemaan jokaisen vuoden säästön nykyarvon erikseen yksittäisen maksun tekijällä.
Vuosisäästöjen lisäksi tätä kerrointa käytetään yleisesti jäännösarvon laskemiseen. Ajatellaanpa ylläolevaa esimerkkiä investoinnista, joka tuottaa 50 000 euroa vuosittain. Jos 10 vuoden päästä koneella onkin jäännösarvoa ja saamme myytyä koneen eteenpäin 25 000 eurolla. Yksittäisen maksun tekijän on 0,3220 ja 25 000 euroa olisi nykyrahassa 8 050 euroa.
Vuosittaiset säästöt ja jäännösarvo ovat nykyrahassa 290 560 euroa. Kone saakin maksaa nyt jo tämän verran.
Jäännösarvoa laskiessa tulee huomata, että koneen jäännösarvo voi olla myös negatiivinen. Mikäli koneella ei ole käyttöä tulevaisuudessa tai sen purkaminen kustantaa enemmän kuin myyntihinta. Jäännösarvon ollessa negatiivinen, se korottaa meidän investointikustannusta.
Annuiteettitekijä
Annuiteettimenetelmässä investointikustannus jaetaan pitoajalle vuosikustannuksiksi. Koneelle lasketaan tavallaan vuosittainen poisto. Tässä menetelmässä annuiteettitekijällä ei kerrota vuosisäästöä vaan investointikustannus.
Kuvitellaan ylläolevan esimerkin koneen investointikustannukseksi 290 000 euroa, joka olisi juuri ja juuri kannattava vuosisäästön ja jäännösarvon jälkeen.
Annuiteettikerroin on 0,1770. Vuosittainen poisto on siis 290 000 € * 0,1770 = 51 330 €.
Koska vuosisäästö on 50 000 €, ei investointi tämän menetelmän mukaan ole kannattava.
Mikäli haluamme annuiteettimenetelmässä laskea mukaan myös jäännösarvon, tulee sen arvo diskontata yksittäisen maksun tekijällä ja vähentää se hankintahinnasta. Tämän jälkeen jäännösarvolla vähennetty hankintahinta jaetaan annuiteettitekijällä vuosittaiseksi kustannukseksi.
[ 290 000€ – (25 000 € * 0,3220) ] * 0,1770 = 49 905,15 €
Huomioimalla jäännösarvo saamme annuiteettimenetelmällä investoinnin vuosituotoksi 94,85 €. Investointi on siis juuri ja juuri kannattava.
Takaisinmaksuaika
Takaisinmaksuaika on erittäin yksinkertainen menetelmä ja yksinkertaisimmillaan se lasketaan investointikustannus / vuosisäästö = takaisinmaksuaika.
Esimerkkimme takaisinmaksuaika on 5,8 vuotta, joten 10 vuoden pitoajalla investointi on hyvinkin kannattava.
Tulee kuitenkin huomata, että tämä yksinkertainen malli ei huomioi tulevien säästöjen diskonttausta. Mikäli haluaa laskea tarkemman takaisinmaksuajan nykyarvojen mukaisesti, tulee vuosittaiset säästöt laskea yksittäisen maksun diskonttauskertoimella ja katsoa kuinka monen vuoden säästöt tähän tarvitaan.
Diskonttaamalla vuosittaiset säästöt, investointimme tuottaa 10 vuodessa vain 282 511 euroa. Lisäämällä tähän jäännösarvon 8 050 e, pääsemme samaan 290 560 € hintaan, jonka jo aiemmin laskimme.
Huomaa, että vuosisäästöjen keskiarvo on 28 251 €, joka on kymmenesosa aiemmin jaksottaisen maksun -kertoimen kautta laskettu nykyarvo.
Korjauskustannukset
Laskelmissa tulee huomata myös mahdolliset korjaus- ja ylläpitokustannukset. Jaksollisen koron menetelmää hyväksikäyttäen on helppo huomioida jatkuvat ylläpitokustannukset. Mikäli kone kuitenkin vaatii ylläpitoajan loppupäässä isompia korjauksia, on meidän käytettävä yksittäisen maksun menetelmää ja laskettava jokaisen vuoden nettosäästö erikseen.
Mahdollisten isompien korjaustöiden kannattavuus on myös hyvä testata investointilaskelmien avulla. Monesti isompi korjaustyö voi pidentää koneen pitoaikaa, joten korjauksen kannnattavuus on helposti laskettavissa samoin kuin alkuperäinen investointikin.
Nyt voit testata investointilaskelmia täällä.



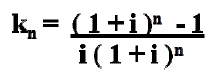

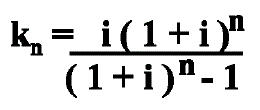




Vastaa