Tilaaminen käytännössä 2, yli- vai alitarjontaa

Olemme tähän mennessä päättäneet tilauserän koon sekä miettineet valmiiksi varmuusvaraston suuruuden. Varmuusvarasto on yksi tapa tyydyttää muuttuva kysyntä, mutta voisimmeko laskea kysynnän jotenkin kysynnän arvon kautta? Aiemmin esitetty varmuusvaraston laskentakaava pohjautui palvelutason määritelmään, nyt keskitytään laskemaan varastoa tuotteen osto- ja myyntihinnan kautta.

Lähtökohta tälle laskentakaavalle on kertakysynnän tarpeisiin vastaaminen. Hyvä esimerkki on joulusesonki. Tehdas valmistaa jotain vain jouluna tarvittavaa tuotetta ja sen kysynnän tiedetään olevan noin 10 000 kpl tuhannen kappaleen hajonnalla. Kysymys kuuluukin, valmistetaanko 9 000, 10 000 vai 11 000 kappaletta? Mikä on näiden eri vaihtoehtojen arvo käytännössä?

Oletetaan, että tuotteen valmistus ja toimitus kauppoihin maksaa 5 €/kpl ja sen myyntihinta on 10 €. Joulun jälkeen ylijääneet tuotteet myydään hintaan 2,50 €/kpl , eikä varastoa säilytetä seuraavaan sesonkiin. Mikäli valmistamme tuotteita enemmän kuin kyseisen vuoden kysyntä on, muodostuu meille 2,5 euron kulu jokaiselta ylituotetulta tuotteelta. Vastaavasti liian pieni tuotanto maksee meille toteutumattomina tuloina 5 euroa tuotteelta.

Lähtöarvot kaavaa varten ovat:

• Ylitarjonta C₀ = 5 – 2,5 = 2,5 €/kpl
• Alitarjonta C_s = 10 – 5 = 5 €/kpl
• Keskikysyntä µ = 10 000 kpl
• Keskihajonta σ = 1 000 kpl
• z kuvaa sitä prosenttia, mikä osa kysynnästä meidän tulisi täyttää
• Q = tuotanto-/hankintamäärä

Kaavat

Yli- vai alitarjontaa?

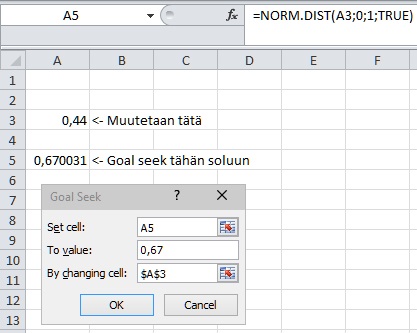
Ensimmäisestä kaavasta saamme arvoksi Φ(z) = 0,67, joka tarkoittaa sitä, että meidän tarvitsee tuottaa tarpeeksi tuotantoa vastaamaan 67 % kysynnästä tai vastaavasti ottaa 33 % riski alitarjonnasta. Tämä Φ-kaava on CDF, eli kumulatiivinen distribuutio funkio, joka voidaan ratkaista esimerkiksi excelissä NORM.DIST-funktiolla ja tavoitehaulla. Alla kuva.

Excel vinkki, tavoitehaku

Oheisesta Excel-ruutukaappauksesta näemme minkälainen kaava solussa A5 on. Kaavaan tulee hakea z-arvo toisesta solusta, jotta voimme muuttaa sitä Excelin tavoitehaulla. Tavoitehaulla haetaan kaavan arvoksi 0,67, joka antaa meille vastaukseksi, että z-arvon tulee olla 0,44. Sijoittamalla tämä kaavaan Q = µ + zσ saamme tuotantomääräksi 10 440 kappaletta. Eli ylituotanto  keskikysyntään verraten on 44 % keskihajonnasta. Jos meidän keskihajonta olisi 2 000 kpl, tällöin tuotantomäärä olisi 10 880 kpl.

Kaava käytännössä

Ylläolevassa esimerkissä siis oletetaan, että alitarjontatilanteessa olisimme saaneet koko 5 € katteen itsellemme, joka nähdään täten kuluna. Todellisuudessa tämä laskutoimitus voi olla hieman monimutkaisempi, joten yrityksen on tarkkaan mietittävä mikä sen todellinen voitto-osuus on myyntihinnasta.

Yhtälailla tätä mallia voidaan käyttää ostoissa. Kauppaan hankittavat lehdet ovat vain päivän, viikon tai kuukauden ajan tuoreita, kunnes tulee seuraava numero. Montako lehteä ostetaan hyllyyn?

Paljonko jäätelöä tilataan hyllyyn?

Hoppin Factory Physics -kirjassa on esimerkki kauppiaasta, joka myy jäätelöä 15 € hintaan. Jäätelön sisäänostohinta on 10 €, sitä toimitetaan viikottain ja kauppias voi tilata jäätelöä minkä määrän tahansa. Viikottainen keskikysyntä myös ei oo -myynti huomioiden on 25 kpl. Tästä kysynnästä meidän pitäisi nyt tietää keskihajonta. Koska meillä ei ole tarpeeksi pitkää historiadataa, oletamme keskihajonnaksi keskikysynnän neliöjuuren (kts. Tilaaminen käytännössä 1).  Neliöjuuri 25:stä on 5 kpl.

Kauppias käyttää laskuissansa 25 % laskentakorkoa, jolloin yhden jäätelöpurkin varastointi maksaa 10 € * (0,25/52) = 0,048 €/viikko. Vastaavasti alitarjonnan kustannus yritykselle on 5 euron menetetty myynti. Tällöin Φ(z) = 5 / (0,048+ 5) = 0,99 ja z arvoksi voimme laskea 2,326. Tällöin optimaalinen viikottainen varastokoko olisi 25 + 2,326 * 5 = 37 kpl.

Kauppiaan tulisi siis tilata jäätelöä viikottain siten, että varastotaso on 37 kpl. Tällöin on optimoitu menetetyn myynnin ja varastoinnin kustannukset.

Oletukset

Tämänkin mallin toteuttaminen pohjaa tiettyihin pohjaoletuksiin:

• Tuote on yksittäinen, eikä se ole sidoksissa mihinkään muuhun tuotteeseen tai sen valmistukseen
• Suunnittelu tehdään yhdelle ajanjaksolle, varastoa ei säilytetä seuraavaan jaksoon
• Kysyntä on satunnaista ja se arvioidaan todennäköisyyslaskennalla
• Tuote toimitetaan/valmistetaan ennalta, toteutuva kysyntä ei vaikuta tuotteen valmistukseen
• Yli- ja alitarjonnan kustannus on lineaarista, tuotteen kpl-kustannus on sama, tehtiin sitä sitten 1 tai 1000 kpl liikaa.

Malli toimii epävarmassa kysynnässä ja varaston määrä riippuu sekä menetetyn myynnin, että ylitarjonnan aiheuttamista kustannuksista sekä keskihajonnasta. Mikäli C_s / ( C₀ + C_s) -kaavan tulos > 0,5 kasvaa tilauskoko keskikysynnästä ja tuloksen ollessa < 0,5 pienenee tilauskoko keskikysynnästä. Toisin sanoen, kun ylitarjonnan kustannus on enemmän kuin menetetty myynti, on tilauskoko tällöin keskikysyntää vähemmän. Mikäli vaihtoehtokustannukset ovat täsmälleen samat, on tällöin tilausmäärä sama kuin keskikysyntä.